有环链表

题目

给定一个链表，如果链表中存在环，则返回到链表中环的起始节点，如果没有环，返回null。

样例

样例 1:

输入：null,no cycle
输出：no cycle
解释：
链表为空，所以没有环存在。

样例 2:

输入：-21->10->4->5，tail connects to node index 1
输出：10
解释：
最后一个节点5指向下标为1的节点，也就是10，所以环的入口为10。

挑战

不使用额外的空间

解题思路

判断有环
首先创建两个指针p1和p2（在Java里就是两个对象引用），让它们同时指向这个链表的头节点。然后开始一个大循环，在循环体中，让指针p1每次向后移动1个节点，让指针p2每次向后移动2个节点，然后比较两个指针指向的节点是否相同。如果相同，则可以判断出链表有环，如果不同，则继续下一次循环
求环长度
当两个指针首次相遇，证明链表有环的时候，让两个指针从相遇点继续循环前进，并统计前进的循环次数，直到两个指针第2次相遇。此时，统计出来的前进次数就是环长。因为指针p1每次走1步，指针p2每次走2步，两者的速度差是1步。当两个指针再次相遇时，p2比p1多走了整整1圈。
因此，环长 = 每一次速度差 × 前进次数 = 前进次数
确定入环点

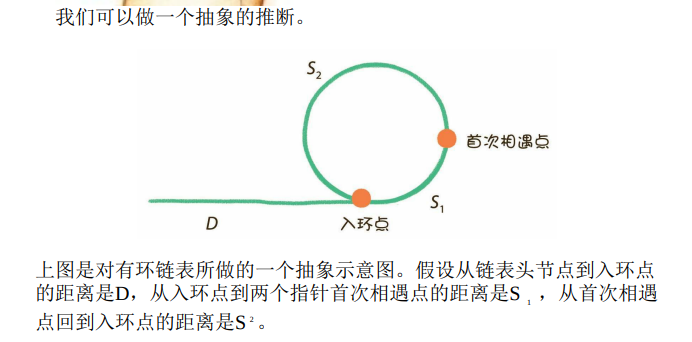
那么，当两个指针首次相遇时，各自所走的距离是多少呢？
指针p1一次只走1步，所走的距离是D+S1
指针p2一次走2步，多走了n(n>=1)整圈，所走的距离是D+S1+n(S2 +S1)。
由于p2的速度是p1的2倍，所以所走距离也是p1的2倍，因此：
2(D+S1 ) = D+S1+n(S1+S2 )
等式经过整理得出：
D = (n-1)(S1+S2) + S2
也就是说，从链表头结点到入环点的距离，等于从首次相遇点绕环n-1圈再回到入环点的距离。
这样一来，只要把其中一个指针放回到头节点位置，另一个指针保持在首次相遇点，两个指针都是每次向前走1步。那么，它们最终相遇的节点，就是入环节点。

源码

/**
 * Definition of singly-linked-list:
 * class ListNode {
 * public:
 *     int val;
 *     ListNode *next;
 *     ListNode(int val) {
 *        this->val = val;
 *        this->next = NULL;
 *     }
 * }
 */

class Solution {
public:
    /**
     * @param head: The first node of linked list.
     * @return: The node where the cycle begins. if there is no cycle, return null
     */
    ListNode * detectCycle(ListNode * head) {
        // write your code here
        
        ListNode * p1,*p2;
        p1=p2=head;
        
        if(p1==NULL)return NULL;
        // if(p1==p1->next)return p1;
        // if(p1->next==NULL)return NULL;
        
        
        bool sign;
        sign = false;
        
        while(p2!=NULL&&p2->next!=NULL){
            p1=p1->next;
            p2=p2->next->next;
            if(p1==p2){
                sign=true;
                break;
            }
        }
        if(sign==false){
            return NULL;
        }
        p1=head;
        
        while(p1!=p2){
            p1=p1->next;
            p2=p2->next;
        }
        return p1;
        
    }
};