1.

题目

在一个无序数组里有99个不重复的正整数，范围是1～100，唯独缺少1个1～100中的整数。如何找出这个缺失的整数？

解答：

先算出1+2+3+…+100的和，然后依次减去数组里的元素，最后得到的差值，就是那个缺失的整数。

复杂度分析

假设数组长度是n，那么该解法的时间复杂度是O(n)，空间复杂度是O(1)。

2.

题目

一个无序数组里有若干个正整数，范围是1～100，其中99个整数都出现了偶数次 ，只有1个整数出现了奇数次 ，如何找到这个出现奇数次的整数？

解答

遍历整个数组，依次做异或运算。由于异或运算在进行位运算时，相同
为0，不同为1，因此所有出现偶数次的整数都会相互抵消变成0，只有
唯一出现奇数次的整数会被留下。

3.

题目

假设一个无序数组里有若干个正整数，范围是1～100，其中有98个整数出现了偶数次，只有2个 整数出现了奇数次，如何找到这2个出现奇数次的整数？

解答

采用分治思想，把数组分成两部分，保证每一部分都包含1个出现奇数次的整数，这样就与上一题的情况一样了。

把2个出现了奇数次的整数命名为A和B。遍历整个数组，然后依次做异或运算，进行异或运算的最终结果，等同于A和B进行异或运算的结果。在这个结果中，至少会有一个二进制位是1（如果都是0，说明A和B相等，和题目不相符）。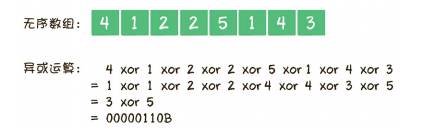
批注 20200614 222045.png
根据这个结论，可以把原数组按照二进制的倒数第2位的不同，分成两部分，一部分的倒数第2位是0，另一部分的倒数第2位是1。由于A和B的倒数第2位不同，所以A被分配到其中一部分，B被分配到另一部分，绝不会出现A和B在同一部分，另一部分既没有A，也没有B的情况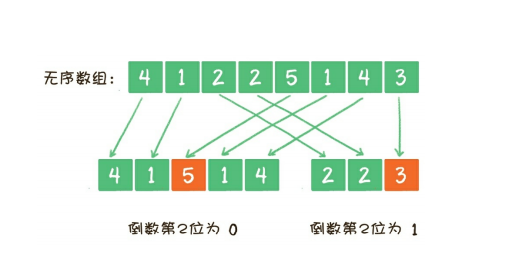
批注 20200614 222127.png

复杂度分析

假设数组长度是n，那么该解法的时间复杂度是O(n)。把数组分成两部分，并不需要借助额外的存储空间，完全可以在按二进制位分组的同时来做异或运算，所以空间复杂度仍然是O(1)。

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
int[] findlostNum(int [] array){
	int result[2]={0,0};
	int xor=0;

	for(int i=0;i<array.length();i++){
		xor^=array[i]
	}

	if(xor==0)
		return Error;

	int separtor = 1;
	while(x==(separtor&xor)){
		separtor<<=1;
	}

	for(int i=0;i<array.length();i++){
		if(1==(separator&array[i])){
			result[1]^=array[i];
		}
		else{
			result[0]^=array[i];
		}
	}
	return result;
}

最后更新： 2022年09月29日 19:37

原始链接： https://yang-xiaofeng1101.github.io/2020/06/14/%E5%AF%BB%E6%89%BE%E7%BC%BA%E5%A4%B1%E7%9A%84%E6%95%B4%E6%95%B0/

赏
× 请我吃糖~
打赏二维码